Polinomlar Konu Anlatımı ve Örnek Soru Çözümü

Polinomlar Konu Anlatımı ve Örnek Soru Çözümü

POLİNOMLAR

a0,a1,a2,a3 …, an ϵ R ve n ϵ N olmak üzere ;

P(x) = a0+a1.x+a2.x2+a3.x3+….+an.xn biçimindeki  ifadelere x değişkenine göre düzenlenmiş reel katsayılı polinom (çok terimli) denir.

an.xn terimindeki an sayısına terimin katsayısı, x’in kuvveti olan n sayısına terimin derecesi

olarak adlandırılır.

Örnek:    P(x) = 8×3 – 3×2 + 4x – 9

1. P(x) polinomunun katsayılarını yazınız: 8,-3,4,-9

1. P(x) polinomunun terimlerini yazınız: 8×3 ,– 3×2 , 4x ,-9

1. P(x) polinomunun baş katsayısını yazınız: 8

1. P(x) polinomunun derecesini yazınız: der [P(x)] = 3

Sabit Polinom

c ϵ R ve c≠0 ( c, 0 dan farklı bir reel sayı ) olmak üzere P(x) = c biçimindeki polinomlar sabit polinom olarak adlandırılır. Sabit polinomun derecesi 0 dır.

Sıfır Polinomu

P(x) = 0 biçimindeki polinomu sıfır polinomu olarak adlandırılır. Sıfır polinomunun derecesi tanımsızdır.

Örnek: P(x) = (2a–3).x2 + b.x + 2.x + 5 ifadesi sabit polinom olduğuna göre a.b çarpımının değerini bulunuz.

Çözüm:

Verilen ifadenin sabit polinom olması için değişkenin olmaması gerekir. Bu sebeple değişkenin katsayısı 0 olmalıdır.

2.a – 3 = 0        ,           x.(b + 2) = 0

2.a = 3                            b + 2 = 0

a = 3/2                            b = – 2

Buradan a.b = – 3

Polinomların Eşitliği

Aynı dereceli terimlerinin katsayıları eşit olan polinomlar eşittir.

Örnek:

P(x) = ax2 + (b – 3)x + 5 Q(x) = – 3×2 + 5x + c + 7

P(x) = Q(x) olduğuna göre a,b,c nin alabileceği değeri bulunuz.

Çözüm:

P(x) = Q(x) ise  ax2 + (b – 3)x + 5 = – 3×2 + 5x + c + 7

• a = – 3
• b – 3 = 5
• b = 8
• c + 7 = 5
• c = – 2

Polinomlarda Dört İşlem

1)  Toplama İşlemi

İki polinom toplanırken; dereceleri aynı olan terimlerin katsayıları kendi aralarında toplanır, o terimin kat sayısı olarak yazılır.

• xn + b. xn = (a + b). xn
• xn + xn = (1+b) . xn

2)  Çıkarma İşlemi

İki polinom çıkarılırken; dereceleri aynı olan terimlerin katsayıları kendi aralarında çıkarılır, o terimin katsayısı olarak yazılır.

3)  Çarpma İşlemi

İki polinomun çarpımı; birisinin her teriminin diğerinin her bir terimi ile ayrı ayrı çarpımlarından elde edilen terimlerin toplamına eşittir.

• axn . bxm = b.xm+n
• xn . bxn = xn+m

4)  Bölme İşlemi

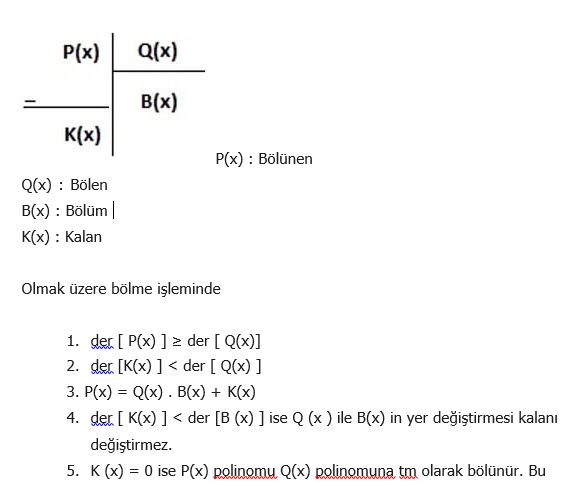 durumda P(x) in çarpanlarından biri Q(x) polinomudur.

Örnek:

Polinomlar Ders Notunu İndirmek İçin Tıklayınız

Kaynak: